Contexte

Python est un langage de programmation très abordable que l’on démarre en programmation ou que l’on connaisse déjà d’autres langages. Néanmoins, ce n’est pas parce qu’un langage est abordable qu’il n’a pas ses propres idiomes et qu’il n’y a pas des trucs & astuces à connaître et à retenir.

Ci-après, une petite note d’apprentissage de Python, sur les compréhensions en Python.

NB : c’est du Python 3 qui est utilisé.

TL;DR

Une compréhension est une manière idiomatique en Python de créer une séquence d’éléments en décrivant comment les éléments de la liste doivent être construits plutôt qu’en construisant une séquence explicitement avec une boucle for ou while. Une compréhension est une expression et peut ainsi être utilisé partout où une valeur ou une expression est attendue.

Une compréhension est constituée par :

  1. une expression fonction de la variable de boucle, expression qui peut être arbitrairement complexe
  2. la définition de la variable de boucle,
  3. le domaine de définition de la variable de boucle

Par exemple, une compréhension de liste des puissances des nombres de 1 à 9 s’écrira :

1

[x**2 for x in range(1, 10)]
  1. x**2 est l’expression : on veut les puissances de 2 de la variable de boucle x
  2. pour la variable x
  3. variable x dont le domaine de définition est l’intervalle des nombres entiers de 1 à 9

Compréhension sans filtre

L’équivalent à la compréhension de liste précédente avec une boucle for classique serait :

1
2
3

powers_of_2 = []
for x in range(1, 10):
    powers_of_2.append(x**2)

Une compréhension peut avoir de manière optionnelle une expression de filtrage qui va permettre d’affiner le domaine de définition de la variable de boucle. Une compréhension est alors constituée par :

  1. une expression fonction de la variable de boucle, expression qui peut être arbitrairement complexe
  2. la définition de la variable de boucle,
  3. le domaine de définition de la variable de boucle
  4. une expression de filtrage

Par exemple, une compréhension de liste des puissances des nombres pairs de 1 à 9 s’écrira :

1

[x**2 for x in range(1, 10) if x % 2 == 0]
  1. x**2 est l’expression : on veut les puissances de 2 de la variable de boucle x
  2. pour la variable x
  3. variable x dont le domaine de définition est l’intervalle des nombres entiers de 1 à 9
  4. seulement si x est un nombre pair.

Compréhension avec filtre

L’équivalent à la liste compréhension avec filtrage précédente avec un for serait :

1
2
3
4

powers_of_2 = []
for x in range(1, 10):
    if x % 2 == 0:
        powers_of_2.append(x**2)

On peut utiliser des compréhensions pour générer des listes, des ensembles et des dictionnaires. Il n’y a pas de compréhension pour les tuples mais vous pouvez créer un générateur à partir d’une compréhension, ce qui peut être utile si vous voulez manipuler des compréhensions infinies.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

# Compréhension de liste
[x**2 for x in range(1, 10)]

# Compréhension d'ensemble
{x**2 for x in range(1, 10)}

# Compréhension de dictionnaire
{x: x**2 for x in range(1, 10)}

# Générateur créé à partir d'une compréhension
(x**2 for x in range(1, 10))

# Générateur "infini" créé à partir d'une compréhension (attention on utilise itertools)
(x**2 for x in itertools.count(1))

# Compréhension de liste avec filtrage
[x**2 for x in range(1, 10) if x % 2 == 0]

Il est possible d’imbriquer les compréhensions même si pour des questions de lisibilité, il n’est pas recommandé de faire des compréhensions avec trop de niveaux d’imbrication (en général il vaut mieux éviter de dépasser 2 niveaux d’imbrication !).

Une compréhension de liste avec 2 niveaux d’imbrication, on pourrait écrire :

1
2
3

columns = ('a', 'b', 'c', 'd', 'e', 'f', 'g', 'h')
rows = (1, 2, 3, 4, 5, 6, 7, 8)
[(c, r) for c in columns for r in rows]

Avec une (double) boucle for, cela serait équivalent à :

1
2
3
4

chessboard = []
for c in columns:
    for r in rows:
        chessboard.append((c, r))

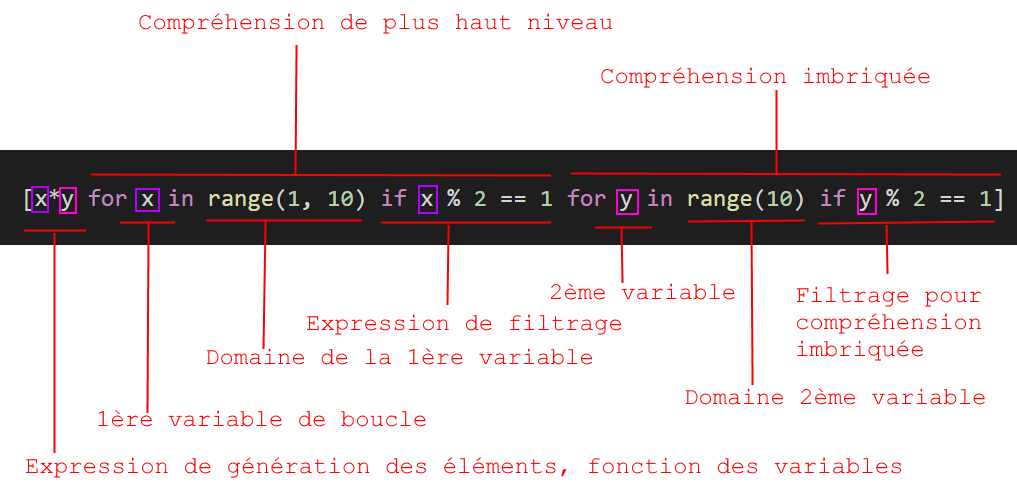
On peut bien sûr avec une clause de filtrage également dans une compréhension imbriquée :

1

[x*y for x in range(1, 10) if x % 2 == 1 for y in range(10) if y % 2 == 1]

Compréhension imbriquée

Le gist avec les sources des exemples.

Pour une bonne compréhension

Détaillons un peu plus ce qui a été présenté au paragraphe précédent.

I have got the power

Pour obtenir une liste des puissances de 2 des chiffres de 1 à 9, on pourrait écrire le code suivant :

1
2
3
4

powers_of_2 = []
for x in range(1, 10):
    if x % 2 == 0:
        powers_of_2.append(x**2)

Néanmoins en Python, il sera plus idiomatique d’écrire cela sous la forme d’une compréhension d’une compréhension de liste, comme suit :

1
2

list_of_powers_of_2_for_first_numbers = [x**2 for x in range(1, 10)]
print(list_of_powers_of_2_for_first_numbers)

Ce qui nous donnera pour la iste dans les 2 cas :

1

[1, 4, 9, 16, 25, 36, 49, 64, 81]

La compréhension est une expression en tant que telle contrairement au for. Elle peut être stockée dans une variable ou directement manipulée comme une liste.

Vous pouvez essayez dans l’interpréteur :

1
2
3
4

>>> sum([x**2 for x in range(1, 10)])
285
>>> [x**2 for x in range(1, 10)][3]
16

Une compréhension est ainsi constituée par :

  1. une expression fonction de la variable de boucle, expression qui peut être arbitrairement complexe
  2. la définition de la variable de boucle,
  3. le domaine de définition de la variable de boucle

Dans l’exemple ci-dessus :

  1. x**2 est l’expression : on veut les puissances de 2 de la variable de boucle x
  2. pour la variable x
  3. variable x dont le domaine de définition est l’intervalle des nombres entiers de 1 à 9

La compréhension de liste de l’exemple peut très littéralement se lire : liste des x à la puissance 2 pour x décrivant l’intervalle des nombres entiers de 1 à 9

Bien sûr l’expression décrivant comment produire chaque élément de la liste peut être arbitrairement complexe et concerner autre chose que des nombres. Sans vouloir souffler le feu et la glace, voici d’autres exemples pour illustrer mon propos :

1
2
3
4
5

lower_case_houses = ["tyrell", "stark",
                     "lannister", "tarly", "baratheon", "targaryen"]
print('Houses in lower case :', lower_case_houses)
capitalized_houses = [(s, s.capitalize()) for s in lower_case_houses]
print(capitalized_houses)

Ce qui donne si on exécute ce code

1
2

Houses in lower case : ['tyrell', 'stark', 'lannister', 'tarly', 'baratheon', 'targaryen']
[('tyrell', 'Tyrell'), ('stark', 'Stark'), ('lannister', 'Lannister'), ('tarly', 'Tarly'), ('baratheon', 'Baratheon'), ('targaryen', 'Targaryen')]

Tous ensemble

Il est possible de générer un ensemble avec une compréhension, ce sont juste les crochets [] délimitant la compréhension qui sont remplacés par des accolades {}.

1
2

set_of_powers_of_2_for_first_numbers = {x**2 for x in range(1, 10)}
print(set_of_powers_of_2_for_first_numbers)

On notera dans le résultat que les éléments de la liste ne sont pas ordonnés, ce qui est normal pour un ensemble.

1

{64, 1, 4, 36, 9, 16, 49, 81, 25}

On sème à tout vent

Comme pour générer un ensemble à partir d’une compréhension, une compréhension pour un dictionnaire utilise des accolades {} à la place des crochets []. En sus, l’expression pour générer les éléments du dictionnaire doit suivre une syntaxe clé: valeur comme dans l’exemple ci-dessous.

1
2

dict_powers_of_2_for_first_numbers = {x: x**2 for x in range(1, 10)}
print(dict_powers_of_2_for_first_numbers)

Ce qui nous donne le dictionnaire ci-après, associant ici le chiffre et son carré.

1

{1: 1, 2: 4, 3: 9, 4: 16, 5: 25, 6: 36, 7: 49, 8: 64, 9: 81}

Benevolent Generator

Les expressions de générateur (generator expressions) font l’objet du PEP289 qui a été accepté pour Python 2.4. Ainsi les expressions de générateur ont été introduites pour proposer une solution basée sur les compréhension performante et efficace en utilisation mémoire. En effet, le constat est que d’une part les compréhensions sont très largement appréciées et utilisées dans la communcauté Python mais que d’autre part les cas d’utilisation typique n’implique pas d’avoir besoin que la liste représentée par la compréhension soit créée entièrement et immédiatemment en mémoire. Il est juste nécessaire de pouvoir itérer sur chaque élément, un élément à la fois.

1
2
3
4
5

generator_of_powers_of_2_for_first_numbers = (x**2 for x in range(1, 10))
print(generator_of_powers_of_2_for_first_numbers)
print(next(generator_of_powers_of_2_for_first_numbers))
print(next(generator_of_powers_of_2_for_first_numbers))
print(*generator_of_powers_of_2_for_first_numbers)

Dans l’exemple ci-dessous, on voit que l’on peut récupérer un élément à la fois, ici via next(). On notera également que l’objet créé est bien un générateur.

1
2
3
4

<generator object <genexpr> at 0x0000018EBF852C10>
1
4
9 16 25 36 49 64 81

Dans le PEP289 il est ainsi recommandé d’utiliser les expressions de générateurs avec des fonctions comme sum(), max() ou min() plutôt que des compréhensions de liste, et de manière générale avec toute fonction réalisant une opération de réduction sur une séquence d’élément.

1
2
3

print(sum((x**2 for x in range(1, 10))))
print(max((x**2 for x in range(1, 10))))
print(min((x**2 for x in range(1, 10))))

Ce qui donne (sans trop de surprise :-)), les résultats suivants.

1
2
3

285
81
1

C’est à retenir. J’avoue que dans le cadre de ce billet, je ne me suis pas fendu de tests de performance pour voir comment l’utilisation ou non d’expressions de compréhension par rapport à des compréhensions de liste impactait l’utilisation de la mémoire et la vitesse d’exécution. Cela serait à effectuer, dans un prochain billet peut-être.

Nous n’en avons pas fini avec les expressions de compréhension, nous allons voir à la prochaine section qu’on peut les utiliser en combinaison avec itertools pour manipuler des séquences infinies.

Infini, dont nous sommes sentinelles

Le module itertools propose des fonctions qui retournent des itérateurs infinis comme count() ou cycle(). Comme avec une expression de générateur on peut itérer sur un élément à la fois, si la source de valeur de notre variable de compréhension est un itérateur infini, on aura une expression de générateurs infinie. Toujours dans itertools, il existe de plus des fonctions qui permettent de manipuler des séquences infinies comme takewhile, qui est utilisé dans l’exemple ci-après.

1
2
3
4
5
6

neverending_generator_of_powers_of_2 = (x**2 for x in itertools.count(1))
print(next(neverending_generator_of_powers_of_2))
print(next(neverending_generator_of_powers_of_2))
print(*itertools.takewhile(lambda x: x < 1000,
                           neverending_generator_of_powers_of_2))
print(next(neverending_generator_of_powers_of_2))

On notera dans les résultats ci-après que les éléments de la séquence sont consommés au fur et à mesure d’abord 2 fois de suite avec la fonction next() puis avec takewhile et enfin à nouveau avec la fonction next(). On notera également que si je peux me permettre ici un unpacking avec * grâce à l’utilisation de takewhile, c’est bien sûr à éviter directement sur une séquence infinie.

1
2
3
4

1
4
9 16 25 36 49 64 81 100 121 144 169 196 225 256 289 324 361 400 441 484 529 576 625 676 729 784 841 900 961
1089

Génération conditionnelle

Les éléments constituant la compréhension peuvent être généré de manière conditionnelle : la séquence est composée du résultat de l’expression qui est fonction de notre variable de compréhension, pour cette variable de compréhension provenant d’une séquence d’élément, si cet élément respecte un certain prédicat.

Par exemple, si je veux avoir la liste des carrés des chiffres pairs, je vais écrire une compréhension de la forme :

1
2
3

list_powers_of_2_for_first_event_numbers = [
    x**2 for x in range(1, 10) if x % 2 == 0]
print(list_powers_of_2_for_first_event_numbers)

Ce qui me donnera la liste de nombres suivantes, correspondant aux carrés de respectivement 2, 4, 6 et 8 :

1

[4, 16, 36, 64]

Bien sûr, le prédicat peut être aussi complexe que nécessaire du moment qu’il est fonction de la variable et qu’il renvoie bien un booléen (une fonction prédicat, quoi ! ;-))

Imbrication

Il est bine sûr possible d’imbriquer les compréhensions de la même manière qu’il est possible d’imbriquer les boucles for. Pour des questions de lisibilité, il n’est pas recommandé de faire des compréhensions avec trop de niveaux d’imbrication (en général il vaut mieux éviter de dépasser 2 niveaux d’imbrication !).

Au début de notre compréhension, on a toujours une expression qui sera ici fonction de l’ensemble des variables de boucle de la compréhension, avec la première compréhension qui correspondrait à notre boucle for la plus interne, puis la seconde, qui correspondrait à la première boucle for imbriquée et ainsi de suite.

Par exemple, si je souhaite avoir une liste de tuple correspondant à la position de chaque case d’un échiquier, je pourrais écrire une compréhension comme suit :

1
2
3
4

columns = ('a', 'b', 'c', 'd', 'e', 'f', 'g', 'h')
rows = (1, 2, 3, 4, 5, 6, 7, 8)
chessboard = [(c, r) for c in columns for r in rows]
print(chessboard)

J’ai une expression fonction de mes variables c et r pour générer les éléments de ma liste (ici juste un tuple), j’ai ensuite le domaine de valeurs que ma variable c décrit pour chaque valeur que décrit ma variable r dans son propre domaine de valeurs. En français cela pourrait donner : la liste est constituée de la pair (c, r) pour c décrivant l’ensemble des valeurs de la liste columns pour chaque r décrivant lui-même l’ensemble des valeurs de la liste rows.

Cela me donne la liste suivante de tuples avec la colonne de l’échiquier en premier élément et la ligne en second :

1

[('a', 1), ('a', 2), ('a', 3), ('a', 4), ('a', 5), ('a', 6), ('a', 7), ('a', 8), ('b', 1), ('b', 2), ('b', 3), ('b', 4), ('b', 5), ('b', 6), ('b', 7), ('b', 8), ('c', 1), ('c', 2), ('c', 3), ('c', 4), ('c', 5), ('c', 6), ('c', 7), ('c', 8), ('d', 1), ('d', 2), ('d', 3), ('d', 4), ('d', 5), ('d', 6), ('d', 7), ('d', 8), ('e', 1), ('e', 2), ('e', 3), ('e', 4), ('e', 5), ('e', 6), ('e', 7), ('e', 8), ('f', 1), ('f', 2), ('f', 3), ('f', 4), ('f', 5), ('f', 6), ('f', 7), ('f', 8), ('g', 1), ('g', 2), ('g', 3), ('g', 4), ('g', 5), ('g', 6), ('g', 7), ('g', 8), ('h', 1), ('h', 2), ('h', 3), ('h', 4), ('h', 5), ('h', 6), ('h', 7), ('h', 8)]

Et bien sûr, si on en a besoin, on peut avoir un filtrage conditionnel des éléments dans une compréhension imbriquée. Par exemple, si je souhaite avoir une liste de la somme de chaque chiffre pair avec chaque chiffres impairs, je pourrais écrire la compréhension suivante avec un filtrage conditionnel :

1
2
3

sum_of_even_and_odd = [
    x + y for x in range(10) if x % 2 == 0 for y in range(10) if y % 2 == 1]
print(sum_of_even_and_odd)

Ce qui me donnera la liste suivante dans laquelle j’ai bien la somme de 0 avec tous les chiffres impairs de 1 à 9, puis la somme de 2 avec tous les chiffres impairs, et ainsi de suite pour tous les chiffres pairs jusqu’à 8.

1

[1, 3, 5, 7, 9, 3, 5, 7, 9, 11, 5, 7, 9, 11, 13, 7, 9, 11, 13, 15, 9, 11, 13, 15, 17]

This is the end, hold your breath and count to ten

Bien sûr pour compter jusqu’à 10, utilisez une compréhension !

Quand on vient à Python d’un autre langage comme Java, les compréhensions sont une nouveauté et leur syntaxe exacte peut être difficile à retenir (surtout si on ne peut pas faire du Python au quotidien) mais une fois qu’on a pris le pli, c’est un outil de Python dont on ne peut plus se passer et que l’on regrette de ne pas avoir dans d’autres langages. Bien sûr tout ce qu’on fait avec des compréhensions, on peut le faire dans le cadre d’un style fonctionnel avec des map et des filter (qui existent également en Python) ou avec des boucles for et des if dans un style impératif (qui existent également en Python), mais il faut reconnaître qu’on peut trouver au compréhension une certaine élégance et une certaine lisibilité (si on n’essaie pas de faire des compréhensions trop imbriquée).

Dans ce billet j’ai essayé de brosser un tableau des compréhensions, de faire une petite synthèse de leur syntaxe et de leurs principales utilisations. En Python, d’après ce que j’ai pu en voir, l’utilisation des compréhensions est considérée comme étant idiomatique au langage. C’est donc un outil que l’on se doit de connaître dès qu’on fait du Python.

J’aurais écrit ce billet sur les compréhensions dans le cadre de mes billets sur Python quoiqu’il arrive mais une demande de Riduidel m’a légèrement fait revoir la priorisation des billets à écrire ;-).

Il y a bien sûr un gist avec les sources des exemples.